Two-colour Counters... because all counters are double sided!
Over the last year or so I have been teaching arithmetic with positive and negative integers using two-colour counters as my model. I sometimes forget that I live in a nice little twitter bubble, and that others haven't had the CPD I have had or the chance to play with these ideas and try them out in classes. As I'm writing this post I am trying think about when the first time I came across two-colour counters was. The ideas I now use in the classroom didn't follow a linear progression anyway, I have pulled ideas from various sources along the way and formed them into a model I am quite happy with, for now (there is always more to lean and always improvements to make). This post is my attempt to communicate how I use two-colour counters in the classroom, both real and virtual, to help my students make sense of arithmetic with negative numbers.
These are the two-colour counters I use in the classroom:

and when I don't have the physical counters or I just want to show something quickly I use the MathsBot ones.
Once we've sorted easy things like show me 3 or 7 or -4 etc. I introduce the zero pair...one counter yellow side up (+1) paired with one counter red side up (-1) make zero.
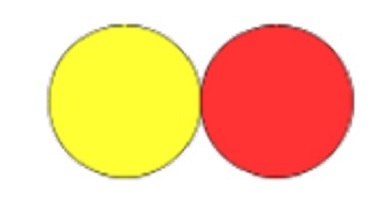
I sometimes introduce zero pairs as part of a pattern too, like in the image below. An idea I took from Mark McCourt's book Teaching for Mastery.

Once they've got the idea of a zero pair we start to look at addition of positive and negative numbers. I want them to spot, and to be fair all of my classes usually do very quickly, that addition of a negative amount gives the same answer as if they'd subtracted that amount. I'll ask some questions like "show me 7" then "Show me 7 – 3" and students will choose to bring in 3 counters red side up and make zero pairs.
This leads nicely to the following sequence of subtractions:
2 – 3 = -1
2 – 2 = 0
2 – 1 = 1
2 – 0 = 2
2 – -1 = ?
In my experience the pattern isn't always enough to convince all pupils and I've found some still heavily rely on the 'takeaway' model of subtraction. So it can be helpful to have some different representations, such as this next one, in case you need them but I tend not to dwell on this one as it neglects the real meaning of subtraction.
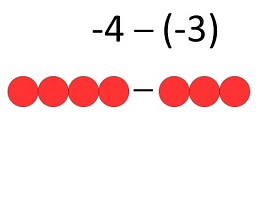
Take, for example, the statement 3 minus negative 2:
3 – - 2
One way to see this is to 'build' 3 using two extra zero pairs so that the two negatives can be removed. When I was first shown this I really liked it, a lot of people still do like this. It's not the way I'd choose to demonstrate this to students any more but, in my opinion, as with any representation, the more you know the better.
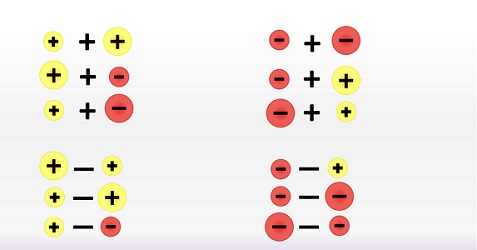
I now choose to spend time talking about additive inverses and how subtraction is shorthand for addition of the additive inverse (as you can see in the series of images above. I know how that sounds but I have genuinely done this with lots of year groups and found this to be the most successful in the long run as it extends so easily into algebra.

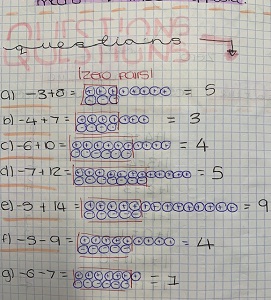
It's important to have an exit strategy with any concrete manipulative and with this it's very easy. Students simply draw counters with 'y' or 'r' inside to represent yellow or red or, as most of mine choose, they draw '+' or '-' signs instead, as you can see the examples above and below. There are some issues to be aware of when doing this though. Because of some of the examples I'd chosen and modelled early on in the lesson, students had misinterpreted that they draw the first number in a row and underneath goes the second number but without checking the signs were making zero pairs, as you can see in the mistake in part f) below.
Eventually we want students to have the sorts of mental models we have for addition and subtraction of negative numbers so tasks which encourage students to consider the size of the numbers and the operation and then determine the size and sign of the answer are really useful here, such as this one, from Don Steward's Median blog, found here which I adapted slightly so that the colours matched those that the students were used to. Jonny Hall's MathsBot also now has an interactive version of this here which is really useful and students really like it.
There are some great tasks on Chris McGrane's site too here
Finally from a practical point of view I use plastic cups to put a useful amount of counters in each for each pair to use. In terms of being careful in the current situation any counters used are only used within the same bubble, and you could get each pair to write a number on the cup so that over a series of lessons they use the same counters. Students, of course, use hand sanitiser before and after using the counters. Over half term I'll be giving the counters a good wash so that they can be used with another group. Ensure that you use enough for students to be able to work on all of the examples you go through. I also use my visualiser to model throughout the lesson.



Using two-colour counters to teach directed number operations is one of the most successful changes I have made to my teaching in recent years and I've used the method with year 7 through to year 11 and I've seen so many lightbulb moments it's been so worth it. I hope this blog is useful to anyone thinking of using the counters and do get in touch on twitter (@mrsHawthorne7) if you want to know any more.