Teaching Place Value

Teaching Place Value...and not just about base ten

I've been teaching nearly ten years, but it is only for the last couple of those that I've actually taught students about place value! I have obviously come across the topic in various schemes or work I've followed over the years but I now realise that all I did was ensure students could do arithmetic in base ten.

I often hear teachers talk about wanting to ensure the maths at secondary school feels different to the maths the students did in primary. I don't think I do. I want them to know it's the same maths, that you can always do even more interesting and fascinating things with maths that may appear the same. So when I teach place value I WANT the students thinking this is the same as what we did in primary and then I'll show them the connections we can make to more complex ideas and build on their understanding. Some people often complain that too many students see mathematics as disconnected procedures to learn but then say things like we want them to do something different in the first few months of secondary. Anyway, that's off topic and probably a blog for another day.

If you only over teach pupils to work in base ten, then I'd argue that you never really teach place value at all. In fact, I think the pupils miss out on some very fundamental ideas of arithmetic. I'd also strongly suggest that a few more pupils might actually understand algebra a little better if we allowed them to build a proper understanding of place value.

This revelation came, for me, when I heard Mark McCourt say he would be surprised if many maths teachers could explain what place value was. I was shocked that I didn't know how to explain this properly.

Take a moment to think about it before reading on. How would you explain place value?

What's the difference between a number, numeral, and a digit? The answer is that that the number is the physical thing or, for me, the idea of that numberness. When I ask you to think of four do you imagine the numeral (4), perhaps the written word 'four' or perhaps you see a collection of objects. The collection of things, that's the number. It's not a mark on paper or a sound, it's a number and it has certain properties, like the way it can be arranged into a square, 2 groups of 2, 1 group of 4. It doesn't matter what base I choose to work in, the number four has those same properties. It is even, it can be arranged into a square, it is not prime. The way I choose to write four, however could change. I could choose to record it like this |||| or 10(base4) or IV (Roman numerals - in fact the Romans would never have done this but that's another story). That's the numeral. The way of recording that number.

In base ten we use the Hindu-Arabic numerals 1 through 9 and a 0. We also use a place value system which means that the position these digits are in a numeral matters and change according to the number we are trying to represent. 123, 132, 213, 231, 312 and 321 are all different numerals, which each represent a different number but use the same digits. In base 10, starting with the right most digit (the units digit) each digit to the left is worth 10 times more than the same digit would be worth if it were in the units place.

So, let's say you're a little intrigued by teaching place value and not just base 10, where do you start? A criticism/concern I often hear is "It would confuse the children" or something else along the lines of it being too hard. I disagree. In a nice way. I understand where the fear/reluctance comes from. For one, and I imagine this is the main reason people omit multi-base arithmetic, it is not tested in most common exams (GCSEs/A-levels) so why bother or waste the time to teach?

Secondly, if a teacher's experience with multi-base arithmetic is limited (which, for most teachers of who have been in the profession for a similar length of time to myself or less, is likely to be the case) then teachers may not feel confident in exploring this area of mathematics with their pupils.

The main purpose of this blog post is to hopefully get those reluctant to teach about multi-base arithmetic ready to explore it for themselves and hopefully then with their students. And then to give those that feel ready to try it a way-in with students with some easy to understand tasks which show that base arithmetic isn't all that hard in the first place.

There were many different base systems that were used before base ten and some would argue, myself included, that the current base ten is far from the best option. There is a lovely history of maths lesson to be had here in terms of the history of why we use base ten.

I begin my first lesson about place value by giving each pair of pupils an amount of counters (random, but definitely more than they could subitise, perhaps around 15-25) and asking how many they have. I watch carefully how the pairs decide to count and arrange theirs. They are deciding how they are going to arrange and count to make it easy for themselves, count in 1s, 2s, a different group size? We discuss this a little and compare different approaches. After this I ask them to arrange the counters so that someone might be able to look at their counters and tell how many there were really quickly. These are the sorts of things they do:

Student's suggestions here are really interesting. Many go for dice patterns. VERY few go for groups of 10 (interesting that isn't it?). I then get students to try a few grouping sizes altogether, so lets all group in 3s or 4s etc and we talk about how we might record how many groups we have and how many leftovers. By showing them on the board a rather large amount of groups I begin to introduce the idea (unless they suggest it first, which has happened) that we could make groups out of the groups. So if we grouped in 4s then every time we get four groups of four we could call that a 'super group' or something. The Heylings textbook, Arithmetic, starts with a task on grouping dots. I've taken inspiration from that to create my task – Bases and Dots

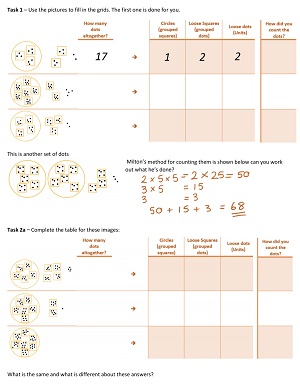
I've done this with a few classes now and of varying abilities and it's worked really well, with lots of discussion about what the digits represent in each case and how easy/hard it is to count different grouping sizes. In the last part of task 2b, where all the numerals are 123, Ashton Coward told me that one of his student's came out with "123 is always x2 +2x +3 where x is the number of dots in a group" well what an insight to gain from what appears to be a simple task!

Task 5 then is how I move away from the dots to a more helpful and efficient representation of numbers in in different bases, dienes blocks. It annoys me greatly that dienes are only widely available in base ten so it is a good job that Jonathan Hall, creator of MathsBot.com, has created virtual dienes which are easy to change to different bases, including imaginary bases for the super geeks, like me, to play with!

Using the dienes as a visual aid we next look at counting in different bases. My favourite thing to ask students is, once they are used to the process, is to count or write down the base 4 numerals for the numbers one to twenty and bet that they all make a mistake (in a nice playful way), which they do at sixteen, because they write it as 40! Sixteen is, of course, the square of the base and would be recorded as 100 in base 4.

Then it depends on the group and their prior experiences but next, I would want students to look at recording numerals in different bases and I'd recommend this great task from Ashton Coward ( @ashtonC94 ). Ashton is a fellow admirer of the book Arithmetic by Paul Lockhart (which is brilliant, by the way) and we spend many hours over most weekends messaging about tasks, especially multi-base tasks. A particularly lovely moment in this task is when pupils get the hang of writing numerals for the numbers one to eighteen in different bases and they get to base 16.

A quote from one of my pupils "Miss, I know that nine will still be 9 and that 10 goes under sixteen so what to I do about this huge gap?". I replied "Oh my goodness, we've run out of numerals. Erm, lets just make some up, I'll use a, b, c, d...". The pupils loved this moment, and I showed them how colours are written in hexadecimal.

After pupils are comfortable with how the numerals work in different bases it is time to do a bit more converting between different bases. I tried to think about other contexts I could bring in this idea of regrouping and so far I have come up with these two tasks around pictograms and packing eggs in boxes.

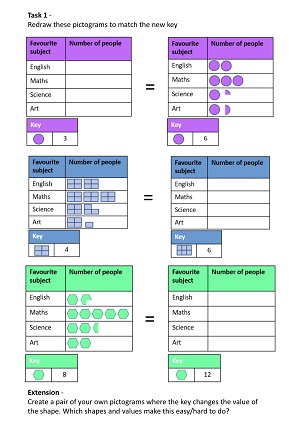
All of these tasks can be found on my resources page

Ashton has also written some lovely tasks around converting from and into base ten. I am sure he will share the full tasks on twitter when he is happy with them but here are a few of my favourite questions:

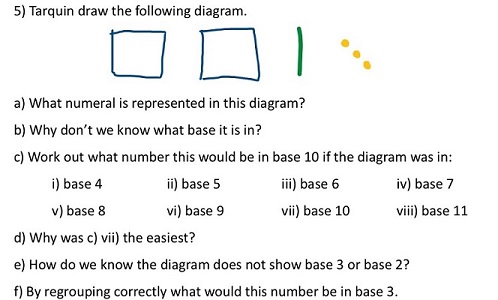
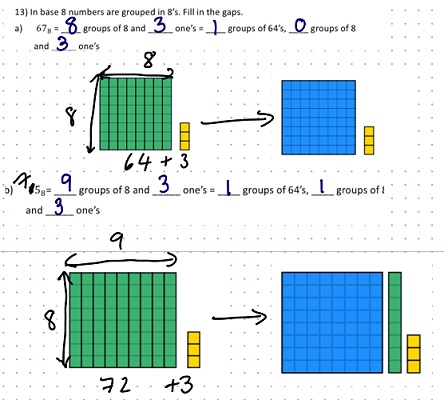
An example of a question from Ashton's bases task about drawing numbers An example of a question about converting and how dienes could help

Then it's time for some really interesting things. Looking at addition and multiplication in different bases. Multiples in different bases are fascinating. Here are some dienes showing multiples of one less than the base (think about the pattern in our nine times table) and some 'one hundred' squares in different bases to look for patterns in multiples.

Multiples of one less than the base in different bases 100 squares in different bases

Bonds to 10 and multiplication squares would look different too. It would be easy to learn times tables if we worked in base three.

Bonds to 10 Multipliaction in base 3

If you want to learn more about place value and arithmetic in different bases there are a few things I would like to recommend:

I hope that this blog has done what it has set out to achieve and encouraged those that haven't taught multi-base arithmetic before to look again at it, but if not I enjoyed writing it. I'll leave you with another quote from Lockhart's Arithmetic.

"Seven times eight is not a question and 56 is not an answer seven times eight is a number, and it is capable of being represented in a great many ways...When we ask, "What is seven times eight?" what we are really asking is, "How can seven groups of eight be rearranged into groups of ten for ease of comparison with other numbers similarly grouped?" Numbers couldn't care less what grouping size you happen to use and neither do mathematicians. Numbers are what they are, they do what they do; your desire to compare is the issue, and your culturally determined choice of representation system is quite secondary. "- Paul Lockhart - Arithmetic